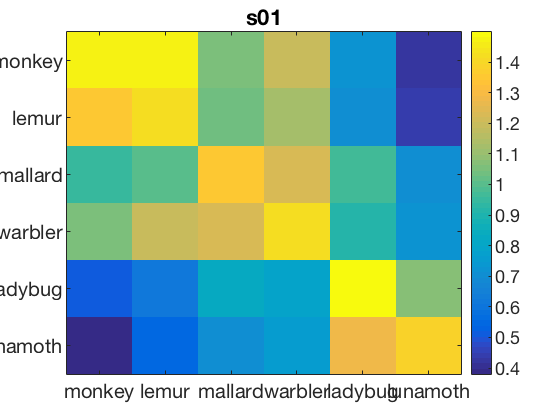
Roi-based MVPA for single subject (run_split_half_correlations_single_sub)

Load t-stat data from one subject, apply 'vt' mask, compute difference of (fisher-transformed) between on- and off diagonal split-half correlation values.

Contents

Set analysis parameters

subject_id = 's01';
roi_label = 'vt'; % 'vt' or 'ev' or 'brain'

config = cosmo_config();
study_path = fullfile(config.tutorial_data_path, 'ak6');

Computations

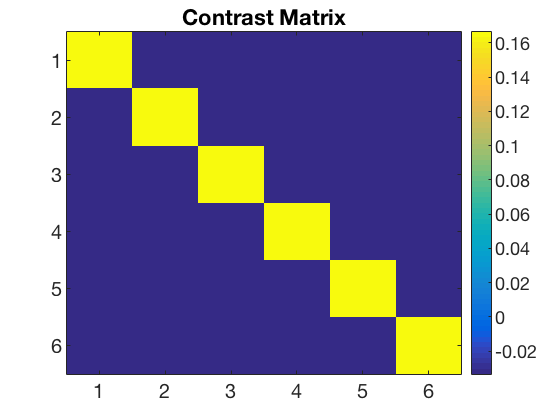
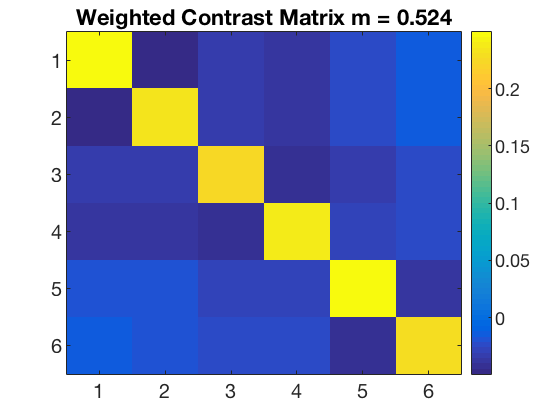
data_path = fullfile(study_path, subject_id);

% file locations for both halves
half1_fn = fullfile(data_path, 'glm_T_stats_odd.nii');
half2_fn = fullfile(data_path, 'glm_T_stats_even.nii');
mask_fn = fullfile(data_path, [roi_label '_mask.nii']);

% load two halves as CoSMoMVPA dataset structs.
half1_ds = cosmo_fmri_dataset(half1_fn, 'mask', mask_fn, ...
                              'targets', (1:6)', ...
                              'chunks', repmat(1, 6, 1));
half2_ds = cosmo_fmri_dataset(half2_fn, 'mask', mask_fn, ...
                              'targets', (1:6)', ...
                              'chunks', repmat(2, 6, 1));

labels = {'monkey'; 'lemur'; 'mallard'; 'warbler'; 'ladybug'; 'lunamoth'};
half1_ds.sa.labels = labels;
half2_ds.sa.labels = labels;

cosmo_check_dataset(half1_ds);
cosmo_check_dataset(half2_ds);

% Some sanity checks to ensure that the data has matching features (voxels)
% and matching targets (conditions)
assert(isequal(half1_ds.fa, half2_ds.fa));
assert(isequal(half1_ds.sa.targets, half2_ds.sa.targets));

nClasses = numel(half1_ds.sa.labels);

% get the sample data
% each half has six samples:
% monkey, lemur, mallard, warbler, ladybug, lunamoth.
half1_samples = half1_ds.samples;
half2_samples = half2_ds.samples;

% compute all correlation values between the two halves, resulting
% in a 6x6 matrix. Store this matrix in a variable 'rho'.
% Hint: use cosmo_corr (or builtin corr, if the matlab stats toolbox
%       is available) after transposing the samples in the two halves.
% >@@>
rho = cosmo_corr(half1_samples', half2_samples');
% <@@<

% Correlations are limited between -1 and +1, thus they cannot be normally
% distributed. To make these correlations more 'normal', apply a Fisher
% transformation and store this in a variable 'z'
% (hint: use atanh).
% >@@>
z = atanh(rho);
% <@@<

% visualize the normalized correlation matrix
figure;
% >@@>
imagesc(z);
colorbar();
set(gca, 'xtick', 1:numel(half1_ds.sa.labels), ...
    'xticklabel', half1_ds.sa.labels);
set(gca, 'ytick', 1:numel(half1_ds.sa.labels), ...
    'yticklabel', half1_ds.sa.labels);
title(subject_id);
% <@@<

% Set up a contrast matrix to test whether the element in the diagonal
% (i.e. a within category correlation) is higher than the average of all
% other elements in the same row (i.e. the average between-category
% correlations). For testing the split half correlation of n classes one
% has an n x n matrix (here, n=6).
%
% To compute the difference between the average of the on-diagonal and the
% average of the off-diagonal elements, consider that there are
% n on-diagonal elements and n*(n-1) off-diagonal elements.
% Therefore, set
% - the on-diagonal elements to 1/n           [positive]
% - the off-diagonal elements to -1/(n*(n-1)) [negative]
% This results in a contrast matrix with weights for each element in
% the correlation matrix, with positive and equal values on the diagonal,
% negative and equal values off the diagonal, and a mean value of zero.
%
% Under the null hypothesis one would expect no difference between the
% average on the on- and off-diagonal, hence correlations weighted by the
% contrast matrix has an expected mean of zero. A positive value for
% the weighted correlations would indicate more similar patterns for
% patterns in the same condition (across the two halves) than in different
% conditions.

% Set the contrast matrix as described above and assign it to a variable
% named 'contrast_matrix'
% >@@>
contrast_matrix = (eye(nClasses) - 1 / nClasses) / (nClasses - 1);

% alternative solution
contrast_matrix_alt = zeros(nClasses, nClasses);
for k = 1:nClasses
    for j = 1:nClasses
        if k == j
            value = 1 / nClasses;
        else
            value = -1 / (nClasses * (nClasses - 1));
        end
        contrast_matrix_alt(k, j) = value;
    end
end

% <@@<

% sanity check: ensure the matrix has a sum of zero
if abs(sum(contrast_matrix(:))) > 1e-14
    error('illegal contrast matrix: it must have a sum of zero');
end

% visualize the contrast matrix
% >@@>
figure;
imagesc(contrast_matrix);
colorbar;
title('Contrast Matrix');
% <@@<

% Weigh the values in the matrix 'z' by those in the contrast_matrix
% (hint: use the '.*' operator for element-wise multiplication).
% Store the result in a variable 'weighted_z'.
% >@@>
weighted_z = z .* contrast_matrix;
% <@@<

% Compute the sum of all values in 'weighted_z', and store the result in
% 'sum_weighted_z'.
% >@@>
sum_weighted_z = sum(weighted_z(:)); % Expected value under H0 is 0
% <@@<

% visualize weighted normalized correlation matrix
figure;
imagesc(weighted_z);
colorbar;
% For the advanced exercise
title(sprintf('Weighted Contrast Matrix m = %5.3f', sum_weighted_z));

Published with MATLAB® R2024a